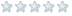quiverkartesisch in polaraxisumgebung

[Momme]

Hallo,
ich möchte in pgfplots in ein poolares Koordinatensystem
mit quiver ein Vektorfeld kartesische eingeben. Als test hatte ich ein Beispiel
mit einem Kartesischen und einen polaren koordiantensystem verglichen, leider kommt nicht das gleiche raus
Ich wollte gerne das poolare Koordinatensystem verwenden, da ich es ganz komfortabel finde, dass ich gleich die Grad Zahlen dabei habe.

mir kommt es so vor, als würde in quiver die Richtung u,v vom Vektor nicht kartesisch sein.

\documentclass[11pt,a4paper,fleqn]{article}
\usepackage[utf8]{inputenc}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{changepage}
\usepackage{booktabs}
\usepackage{geometry}
\usepackage{hyperref}
\usepackage{ifthen}
\usepackage{todonotes}
\usepackage[ngerman]{babel}
\geometry{a4paper, top=30mm, left=30mm, right=30mm, bottom=30mm,
headsep=10mm, footskip=12mm}
\setlength\mathindent{0 cm}

\usepackage{tikz}
\usepackage{pgfplots}
\pgfplotsset{compat=newest}
\usetikzlibrary{calc,intersections,matrix,arrows,pgfplots.polar}
\usepgfplotslibrary{polar}
\begin{document}
\begin{tikzpicture}
	\begin{polaraxis}[width=300pt,xtick={0,30,...,330},
	ytick={0,1,1.5},
	major grid style={dotted},  
	minor grid style={dotted},  
	minor x tick num=1,
	minor y tick num=1,
	]
	%\addplot [domain=0:5] (x,sin(2*x)); % (angle,radius)
	%		\addplot coordinates {(180,2) (0,0)};
	\addplot[data cs=cart,samples=20, domain=0:360,
	% the default choice ’variable=\x’ leads to
	% unexpected results here!
	variable=\t,
	quiver={
		u={-sin((t))},
		v={cos((t))},
		scale arrows=0.5},
	->,blue]
	({cos((t))}, {sin((t))});
	\end{polaraxis}
\end{tikzpicture}
	\\
\begin{tikzpicture}
	\begin{axis}[axis equal,
	axis lines=middle,
	axis line style={->},
	tick style={color=black},
	xtick=\empty,
	ytick=\empty
	]
	\addplot[samples=20, domain=0:2*pi,
	% the default choice ’variable=\x’ leads to
	% unexpected results here!
	variable=\t,
	quiver={
		u={-sin(deg(t))},
		v={cos(deg(t))},
		scale arrows=0.5},
	->,blue]
	({cos(deg(t))}, {sin(deg(t))});
	\addplot[samples=100, domain=0:2*pi]
	({cos(deg(x))}, {sin(deg(x))});
	\end{axis}
\end{tikzpicture}
\end{document}

[Momme]

Ich habe mir jetzt zur Lösung des Problems einfach selber ein Kreisdiagramm in der Axis Umgebung gezeichnet. Falls jemand das gleiche Problem haben sollte poste ich meinen Code:

\documentclass[11pt,a4paper,fleqn]{article}
\usepackage[utf8]{inputenc}
\usepackage{amsmath}
\usepackage{changepage}
\usepackage{booktabs}
\usepackage{geometry}
\usepackage{hyperref}
\usepackage{ifthen}
\usepackage{todonotes}
\usepackage[ngerman]{babel}
\geometry{a4paper, top=30mm, left=30mm, right=30mm, bottom=30mm,
headsep=10mm, footskip=12mm}
\setlength\mathindent{0 cm}

\usepackage{tikz}
\usepackage{pgfplots}
\pgfplotsset{compat=newest}
\usetikzlibrary{calc,intersections,matrix,arrows,pgfplots.polar}
\usepgfplotslibrary{polar}
\begin{document}
\begin{tikzpicture}
	\begin{axis}[axis equal,width=400pt,clip=false,
	axis lines=middle,
	hide x axis, hide y axis
	]
	\addplot[dotted,samples=100, domain=0:2*pi]
	({cos(deg(x))}, {sin(deg(x))});
	\addplot[dotted,samples=100, domain=0:2*pi]
	({0.25*cos(deg(x))}, {0.25*sin(deg(x))});
	\addplot[dotted,samples=100, domain=0:2*pi]
	({0.5*cos(deg(x))}, {0.5*sin(deg(x))});
	\addplot[dotted,samples=100, domain=0:2*pi]
	({0.75*cos(deg(x))}, {0.75*sin(deg(x))});
	\addplot[samples = 100,domain=0:360] ({1.1*cos(x)},{1.1*sin(x)});
	\addplot [dotted,data cs=polar] coordinates{(0,0) (0,1.1)};
	\addplot [dotted,data cs=polar] coordinates{(30,0) (30,1.1)};
	\addplot [dotted,data cs=polar] coordinates{(60,0) (60,1.1)};
	\addplot [dotted,data cs=polar] coordinates{(90,0) (90,1.1)};
	\addplot [dotted,data cs=polar] coordinates{(120,0) (120,1.1)};
	\addplot [dotted,data cs=polar] coordinates{(150,0) (150,1.1)};
	\addplot [dotted,data cs=polar] coordinates{(180,0) (180,1.1)};
	\addplot [dotted,data cs=polar] coordinates{(210,0) (210,1.1)};
	\addplot [dotted,data cs=polar] coordinates{(240,0) (240,1.1)};
	\addplot [dotted,data cs=polar] coordinates{(270,0) (270,1.1)};
	\addplot [dotted,data cs=polar] coordinates{(300,0) (300,1.1)};
	\addplot [dotted,data cs=polar] coordinates{(330,0) (330,1.1)};
	
	\addplot [data cs=polar] coordinates{(0,1.1) (0,1.15)};
	\addplot [data cs=polar] coordinates{(30,1.1) (30,1.15)};
	\addplot [data cs=polar] coordinates{(60,1.1) (60,1.15)};
	\addplot [data cs=polar] coordinates{(90,1.1) (90,1.15)};
	\addplot [data cs=polar] coordinates{(120,1.1) (120,1.15)};
	\addplot [data cs=polar] coordinates{(150,1.1) (150,1.15)};
	\addplot [data cs=polar] coordinates{(180,1.1) (180,1.15)};
	\addplot [data cs=polar] coordinates{(210,1.1) (210,1.15)};
	\addplot [data cs=polar] coordinates{(240,1.1) (240,1.15)};
	\addplot [data cs=polar] coordinates{(270,1.1) (270,1.15)};
	\addplot [data cs=polar] coordinates{(300,1.1) (300,1.15)};
	\addplot [data cs=polar] coordinates{(330,1.1) (330,1.15)};
	\addplot [->,data cs=polar] coordinates{(0,0) (0,1.05)}
	[yshift=-12pt]
	node[pos=0]{$\displaystyle 0$}
	node[pos=0.95]{$\displaystyle R_0$};
	\node at (axis cs:{1.25*cos(0)},{1.25*sin(0)}) {$\displaystyle0$};
	\node at (axis cs:{1.25*cos(30)},{1.25*sin(30)}) {$\displaystyle\frac{1}{6}\pi$};
	\node at (axis cs:{1.25*cos(60)},{1.25*sin(60)}) {$\displaystyle\frac{2}{6}\pi$};
	\node at (axis cs:{1.25*cos(90)},{1.25*sin(90)}) {$\displaystyle\frac{3}{6}\pi$};
	\node at (axis cs:{1.25*cos(120)},{1.25*sin(120)}) {$\displaystyle\frac{4}{6}\pi$};
	\node at (axis cs:{1.25*cos(150)},{1.25*sin(150)}) {$\displaystyle\frac{5}{6}\pi$};
	\node at (axis cs:{1.25*cos(180)},{1.25*sin(180)}) {$\displaystyle\pi$};
	\node at (axis cs:{1.25*cos(210)},{1.25*sin(210)}) {$\displaystyle1\frac{1}{6}\pi$};
	\node at (axis cs:{1.25*cos(240)},{1.25*sin(240)}) {$\displaystyle1\frac{2}{6}\pi$};
	\node at (axis cs:{1.25*cos(270)},{1.25*sin(270)}) {$\displaystyle1\frac{3}{6}\pi$};
	\node at (axis cs:{1.25*cos(300)},{1.25*sin(300)}) {$\displaystyle1\frac{4}{6}\pi$};
	\node at (axis cs:{1.25*cos(330)},{1.25*sin(330)}) {$\displaystyle1\frac{5}{6}\pi$};
	\addplot[samples at={0,pi/6,...,2*pi}, variable=\t,	quiver={
		u={-sin(deg(t))},	v={cos(deg(t))},	scale arrows=0.2}, ->,blue]
	({cos(deg(t))}, {sin(deg(t))});
	\addplot[samples at={0,pi/6,...,2*pi},
	variable=\t,
	quiver={
		u={-0.5*sin(deg(t))},
		v={0.5*cos(deg(t))},
		scale arrows=0.2},
	->,blue]
	({0.5*cos(deg(t))}, {0.5*sin(deg(t))});
	\addplot[samples at={0,pi/6,...,2*pi},
	variable=\t,
	quiver={
		u={-0.75*sin(deg(t))},
		v={0.75*cos(deg(t))},
		scale arrows=0.2},
	->,blue]
	({0.75*cos(deg(t))}, {0.75*sin(deg(t))});	
	\addplot[samples at={0,pi/6,...,2*pi},
	variable=\t,
	quiver={
		u={-0.25*sin(deg(t))},
		v={0.25*cos(deg(t))},
		scale arrows=0.2},
	->,blue]
	({0.25*cos(deg(t))}, {0.25*sin(deg(t))});			
	\end{axis}
\end{tikzpicture}

\end{document}