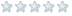Symbol für gedrehten Vektor

[Spiro]

Hallo,

ich such nach dem Symbol, mit dem man gedrehte Vektoren darstellt.
Ähnlich wie \urcorner ,nur, dass unter dieses Zeichen nun noch ein Buchstabe muss. Im Endeffekt wie \overline{v} mit einem Hacken rechts nach unten.
Hab schon "The Comprehensive LATEX Symbol List" von Scott Pakin durchgewälzt, aber nichts gefunden.

Danke schonmal für die Hilfe!
Spiro

[localghost]

Was genau meinst Du mit einem "gedrehten" Vektor? Einen transponierten Vektor? Wie auch immer, eine solche Darstellung, wie Du sie beschreibst, ist mir noch nie begegnet.


Thorsten

[iTob]

Hallo,

auch wenn ich ebenfalls nicht den Sinn verstehe, hab ich mal ein Bisschen gebastelt und das folgende hingefrickelt. Problem: Der Akzent sitzt zu tief, aber vielleicht weiß ja jemand, wie man den höher rücken kann...

\documentclass[11pt,a4paper]{scrartcl}
\usepackage[latin1]{inputenc}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{amssymb}
%\newcommand{\tvec}[1]{#1\kern-0.35em\lower-0.3ex\hbox{$\urcorner$}}
%\newcommand{\uneg}{\mathrel{\mbox{\raisebox{0.6ex}{$\neg$}}}}
\newcommand{\uneg}{\neg}
\newcommand{\tvec}[1]{\ensuremath{\mathaccent\uneg #1}}
\begin{document}
Eigener Befehl für gedrehte Vektoren:
\begin{equation}
\vec{a}=\tvec{b}= % \frac{\tvec{r}}{\tvec{k}}= B^\tvec{y}= % A_{\tvec{x}}=\int_{\tvec{\alpha}}^\tvec{\xi}
\end{equation}
\begin{equation}
\tvec{a}\quad\tvec{b}\quad\tvec{c}\quad\tvec{d}\quad
\tvec{e}\quad\tvec{f}\quad\tvec{g}\quad\tvec{h}\quad
\tvec{i}\quad\tvec{j}\quad\tvec{k}\quad\tvec{l}\quad
\tvec{m}\quad\tvec{n}\quad\tvec{o}\quad\tvec{p}\quad
\tvec{q}\quad\tvec{r}\quad\tvec{s}\quad\tvec{t}\quad
\tvec{u}\quad\tvec{v}\quad\tvec{w}\quad\tvec{x}\quad
\tvec{y}\quad\tvec{z}\quad
\end{equation}
\end{document}

[iTob]

So Versuch 2 scheint mir besser gelungen und eleganter zu sein:

\documentclass[11pt,a4paper]{scrartcl}
\usepackage[latin1]{inputenc}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{accents}
% siehe: http://www.cs.brown.edu/system/software/latex/doc/accents.pdf
% neuer Befehl (tvec für turned vector):
\newcommand{\tvec}[1]{\ensuremath{\accentset{\neg}{#1}}}
\begin{document}
Eigener Befehl für gedrehte Vektoren:
\begin{equation}
\vec{a}\ \tvec{a} = \vec{d}\ \tvec{d}
\end{equation}
\begin{equation}
\tvec{a}\quad\tvec{b}\quad\tvec{c}\quad\tvec{d}\quad
\tvec{e}\quad\tvec{f}\quad\tvec{g}\quad\tvec{h}\quad
\tvec{i}\quad\tvec{j}\quad\tvec{k}\quad\tvec{l}\quad
\tvec{m}\quad\tvec{n}\quad\tvec{o}\quad\tvec{p}\quad
\tvec{q}\quad\tvec{r}\quad\tvec{s}\quad\tvec{t}\quad
\tvec{u}\quad\tvec{v}\quad\tvec{w}\quad\tvec{x}\quad
\tvec{y}\quad\tvec{z}\quad
\end{equation}
\end{document}

Viele Grüße...

[Spiro]

Hallo iTob,

vielen Dank! So funktionierts!

In der Getriebetechnik kann man für Koppelgetriebe beispielsweise mit Hilfe des sog. "graphischen Vektorverfahrens" die Geschwindigkeiten und Beschleunigungen der einzelnen Getriebeglieder in einer bestimmten Getriebestellung ermitteln. Um nun beispielsweise mit der Geschwindigkeit des Antriebs schrittweise die Beschleunigung am Abtrieb herzuleiten, muss der Geschwindigkeitsvektor erst einmal um 90° gedreht werden, bevor man fortfahren kann. Der Ausdruck "gedrehter Vektor" ist hier ein feststehender Begriff.

Wünsche noch einen schönen Sonntagabend!
Spiro

[iTob]

ah, ok, wenn alle wissen, was ein gedrehter Vektor ist, ist es ja kein Problem. Ist den diese Kennzeichnung auch üblich?

Wie wird es denn im Englischen genannt? Dann könntest du danach nochmal im Zusammenhang mit LaTeX googlen und schauen, ob es eine bessere/andere Lösung gibt...

[Spiro]

es gibt hier tatsächlich mehrere Möglichkeiten zur Kennzeichnung; an der Bildungseinrichtung, an der ich tätig bin, ist dies die gebräuchliche.

der "gedrehte Vektor" oder "gedrehte Geschwindigkeitsvektor" wird im Englischen als "orthogonal velocity vector" bezeichnet.
das ist die laut IFToMM (International Federation for the Theory of Machines and Mechanisms) Commission A Standards for Terminology (1996) gültige internationale Bezeichnung

Grüße,
Spiro

[Spiro]

... ach ja: Deine Lösung ist hervorragend! Da muss ich nicht mehr googeln!