TikZ/pgfplots: node pos nur anhand von Abzisse
Verfasst: So 30. Jul 2017, 12:15
Hallo liebes Forum,
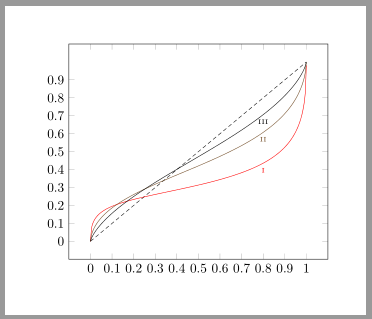
folgende Frage beschäftigt mich. Ich habe eine Funktion, bei der ich die Auswirkungen unterschiedlicher Parameter zeigen möchte. Also plotte ich die Funktion in pgfplots mit jeweils unterschiedlichen Einstellungen. Jetzt möchte ich die drei Varianten mit I, II und III beschriften. Dazu benutze ich die Einstellung pos=<Wert>. So wie ich das verstehe, berechnet TikZ intern die Länge vom Plot und setzt den Node dann an die entsprechende Stelle. Ich würde aber gerne, dass die Nodes in Abhängigkeit vom Abzissenwert (x-Achse) gesetzt werden. Denn das Problem ist, dass Funktionen, die stärker oszillieren, von TikZ eine größere Länge bekommen. Daher bedeutet pos=<Wert> für jeden Plot etwas anderes. Im Prinzip suche ich so etwas wie "x pos=<Wert>". Hat jemand mein Problem verstanden und kann mir helfen? Hier ein MWE:
Zusatzfrage: Warum verschwindet der letzte y-Tick, wenn ich wie im Code explizit angebe, wie die Ticks laufen sollen? Um das Problem zu umgehen, verwende ich bis dato immer einen leicht höheren Wert für den letzten Tick, damit er erscheint. In diesem Fall erscheint der x-Tick bei 1, nicht aber der y-Tick.
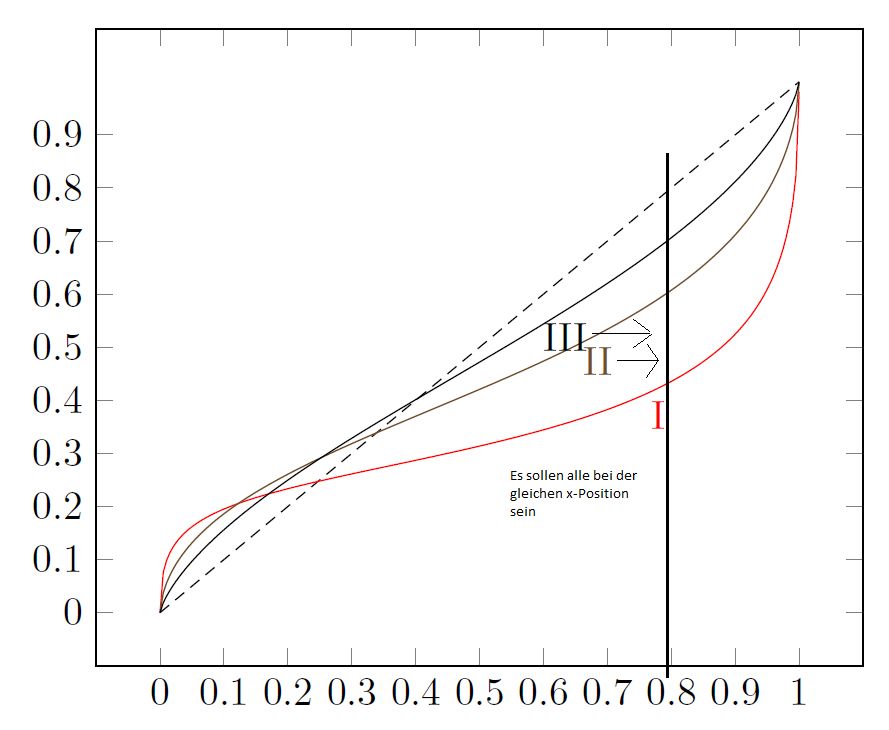
folgende Frage beschäftigt mich. Ich habe eine Funktion, bei der ich die Auswirkungen unterschiedlicher Parameter zeigen möchte. Also plotte ich die Funktion in pgfplots mit jeweils unterschiedlichen Einstellungen. Jetzt möchte ich die drei Varianten mit I, II und III beschriften. Dazu benutze ich die Einstellung pos=<Wert>. So wie ich das verstehe, berechnet TikZ intern die Länge vom Plot und setzt den Node dann an die entsprechende Stelle. Ich würde aber gerne, dass die Nodes in Abhängigkeit vom Abzissenwert (x-Achse) gesetzt werden. Denn das Problem ist, dass Funktionen, die stärker oszillieren, von TikZ eine größere Länge bekommen. Daher bedeutet pos=<Wert> für jeden Plot etwas anderes. Im Prinzip suche ich so etwas wie "x pos=<Wert>". Hat jemand mein Problem verstanden und kann mir helfen? Hier ein MWE:
\documentclass[border=1cm]{standalone}
\usepackage{tikz,pgfplots}
\pgfplotsset{compat=newest}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
domain=0:1,
samples=200,
xtick={0,0.1,...,1.01}, %Zusatzfrage
ytick={0,0.1,...,1},
no marks,
]
\addplot [densely dashed] {x};
\addplot {(x^.45)/(x^.45+(1-x)^.45)^(1/.45))} node [pos=.6,below] {I};
\addplot {(x^.61)/(x^.61+(1-x)^.61)^(1/.61))} node [pos=.6,below] {II};
\addplot {(x^.75)/(x^.75+(1-x)^.75)^(1/.75))} node [pos=.6,below] {III};
\end{axis}
\end{tikzpicture}
\end{document}