von RobertS » Mo 1. Aug 2016, 14:59
Hallo Leute,
das folgende Problem bringt mich grade zum verzweifeln. Ich habe mit Mühe und Not das folgende Optimierungsproblem zu meiner Zufriedenheit formatiert. Was fehlt ist jetzt eine Nummerieung der einzelnen Nebenbedingungen.
\begin{subequations} \label{ocp:simple}
\begin{align}
\underset{x, u }{\text{min}} & \int_{0}^{1} \Phi(t, x(t), u(t)) dt \\
\text{s.t.}&
\begin{aligned}[t]
\dot{x}(t) &= f(t,x(t),u(t)), & t \in \left[0,1 \right] \\
\sum\limits_{j=0}^Mr_j(x(t_j)) &= 0& \\
g(t,x(t),u(t)) & \geq 0 , & t \in \left[0, 1 \right] \label{ocp:simple:pathcon}
\end{aligned}
\end{align}
\end{subequations}
Auf dem Screenshot im Anhang sieht man wie der gesetzte Code ausschaut.
Wie bekomme ich die fehlende Nummerierung hin?
Anmerkung: Das für mich schwierige an der Sache war, dass die Nebenbedingungen ihre eigene Ausrichtung haben, von der die Zielfunktion etc nicht betroffen ist. Vielleicht gibt es dafür ja auch andere Lösungen. Bin für alles offen.
Vielen Dank schon mal im Vorraus
- Dateianhänge
-
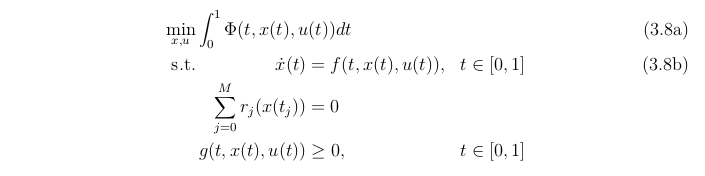
- Code gesetzt!
- 2016-08-01-145658_705x176_scrot.png (14.51 KiB) 2661 mal betrachtet
Hallo Leute,
das folgende Problem bringt mich grade zum verzweifeln. Ich habe mit Mühe und Not das folgende Optimierungsproblem zu meiner Zufriedenheit formatiert. Was fehlt ist jetzt eine Nummerieung der einzelnen Nebenbedingungen.
[code]
\begin{subequations} \label{ocp:simple}
\begin{align}
\underset{x, u }{\text{min}} & \int_{0}^{1} \Phi(t, x(t), u(t)) dt \\
\text{s.t.}&
\begin{aligned}[t]
\dot{x}(t) &= f(t,x(t),u(t)), & t \in \left[0,1 \right] \\
\sum\limits_{j=0}^Mr_j(x(t_j)) &= 0& \\
g(t,x(t),u(t)) & \geq 0 , & t \in \left[0, 1 \right] \label{ocp:simple:pathcon}
\end{aligned}
\end{align}
\end{subequations}
[/code]
Auf dem Screenshot im Anhang sieht man wie der gesetzte Code ausschaut.
Wie bekomme ich die fehlende Nummerierung hin?
Anmerkung: Das für mich schwierige an der Sache war, dass die Nebenbedingungen ihre eigene Ausrichtung haben, von der die Zielfunktion etc nicht betroffen ist. Vielleicht gibt es dafür ja auch andere Lösungen. Bin für alles offen.
Vielen Dank schon mal im Vorraus