von cis » Mi 26. Aug 2020, 12:34
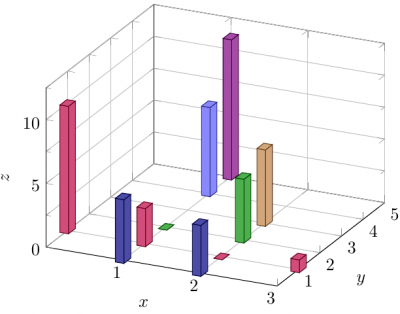
Ungeachtet des Umstandes, dass das eine perspektivisch verwirrende Darstellung ist, kann man mit pgfplots ein 3D-Bardiagramm so erstellen:
Die Idee ist mark=cube* zu verwenden und die cube/size z so zu manipulieren, dass die gewünschten 3D-Bars entstehen.
Setzt man z.B. cube/size z=4mm, so dimensioniert das Würfelchen von seiner Raumposition aus um 2mm und um -2mm in z-Richtung.
Also müssen sie bei x=X, y=Y, z expr={0.5*\thisrow{Z}} positioniert werden.
Die richtige Höhe der cubes kann mit
visualization depends on={\thisrow{Z} \as \zvalue},
scatter/@pre marker code/.append style={
/utils/exec=\pgfmathsetmacro{\barheight}{\zunitlength*\zvalue},
/pgfplots/cube/size z=\barheight
},
bestimmt werden, wobei die zunitlength mit
\path let \p1=($(axis cs:0,0,1)-(axis cs:0,0,0)$) in
\pgfextra{ \pgfmathsetglobalmacro{\zunitlength}{\y1} } };
gemessen werden kann.
€dit: Es zeigt sich, dass es sinnvoll ist zmax=\zMax zu setzen, dazu kann der maximale z-Wert in der Form
\pgfplotstablegetrowsof{\datatable}
\pgfmathtruncatemacro{\RowsNo}{\pgfplotsretval-1}
%Zeilenzahl: \RowsNo
\pgfmathsetmacro\zMax{0}
\foreach \n in {0,...,\RowsNo}{
\pgfplotstablegetelem{\n}{Z}\of{\datatable}
\pgfmathparse{\pgfplotsretval > \zMax ? \pgfplotsretval : \zMax}
\xdef\zMax{\pgfmathresult}
}
%Maximalwert z-Achse: \zMax
ermittelt werden.
\documentclass[border=5pt, tikz]{standalone}
\usepackage{pgfplots}
\usepackage{pgfplotstable}
\pgfplotsset{compat=1.17}
\usetikzlibrary{calc}
\def\pgfmathsetglobalmacro#1#2{\pgfmathparse{#2}%
\global\let#1\pgfmathresult}
\pgfplotsset{
colormap = {mycolormap}{
color(0) = (blue!50!black);
color(1) = (purple);
color(2) = (green!55!black);
color(3) = (brown);
color(4) = (blue!66)
color(5) = (violet)
},
colormap name=mycolormap,
%colormap name=viridis
}
\begin{document}
\pgfplotstableread[col sep=comma,header=true]{
X, Y, Z
2, 0, 4
1, 0, 5
0, 1, 10
3, 1, 1
1, 1, 3
2, 1, 0
1, 2, 0
2, 2, 5
2, 3, 6
1, 4, 7
1, 5, 11
}{\datatable}
% z-Maximum determination ==================
\pgfplotstablegetrowsof{\datatable}
\pgfmathtruncatemacro{\RowsNo}{\pgfplotsretval-1}
%Number of rows: \RowsNo
\pgfmathsetmacro\zMax{0}
\foreach \n in {0,...,\RowsNo}{
\pgfplotstablegetelem{\n}{Z}\of{\datatable}
\pgfmathparse{\pgfplotsretval > \zMax ? \pgfplotsretval : \zMax}
\xdef\zMax{\pgfmathresult}
}
%Maximum z-Axis: \zMax
% ============================
\begin{tikzpicture}[]
\begin{axis}[
%height=2cm, width=7cm,
% view={120}{40}, x dir=reverse,
xmin=0,
ymin=0,
zmin=0, zmax=\zMax,
enlarge z limits={rel=0.25,upper},
xtick={1,...,10},
ytick={1,...,10},
%ytick={0,25,...,100},
grid=both,
xlabel={$x$}, ylabel={$y$}, zlabel={$z$},
minor z tick num=1,
point meta=explicit,
scatter/use mapped color={draw=mapped color!50!black,
fill=mapped color!70},
]
% unitlenghth z-Axis determination
\path let \p1=($(axis cs:0,0,1)-(axis cs:0,0,0)$) in
\pgfextra{ \pgfmathsetglobalmacro{\zunitlength}{\y1} } node[xshift=2cm, yshift=2cm]{%\zunitlength % show value
};
\addplot3[
scatter, only marks,
mark=cube*, mark size=5, %opacity=0.8,
nodes near coords*=, % will er...
%%% barheight determination
visualization depends on={\thisrow{Z} \as \zvalue},
scatter/@pre marker code/.append style={
/utils/exec=\pgfmathsetmacro{\barheight}{\zunitlength*\zvalue},
/pgfplots/cube/size z=\barheight
},
] table[x=X, y=Y,
z expr={0.5*\thisrow{Z}},
meta expr={\thisrow{Y}}
]{\datatable};
\end{axis}
\end{tikzpicture}
\end{document}Ungeachtet des Umstandes, dass das eine perspektivisch verwirrende Darstellung ist, kann man mit pgfplots ein 3D-Bardiagramm so erstellen:
Die Idee ist [tt]mark=cube*[/tt] zu verwenden und die [tt]cube/size z[/tt] so zu manipulieren, dass die gewünschten 3D-Bars entstehen.
Setzt man z.B. [tt]cube/size z=4mm[/tt], so dimensioniert das Würfelchen von seiner Raumposition aus um 2mm und um -2mm in z-Richtung.
Also müssen sie bei [tt]x=X, y=Y, z expr={0.5*\thisrow{Z}}[/tt] positioniert werden.
Die richtige Höhe der cubes kann mit
[tt]visualization depends on={\thisrow{Z} \as \zvalue},
scatter/@pre marker code/.append style={
/utils/exec=\pgfmathsetmacro{\barheight}{\zunitlength*\zvalue},
/pgfplots/cube/size z=\barheight
},[/tt]
bestimmt werden, wobei die [tt]zunitlength[/tt] mit
[tt]\path let \p1=($(axis cs:0,0,1)-(axis cs:0,0,0)$) in
\pgfextra{ \pgfmathsetglobalmacro{\zunitlength}{\y1} } };
[/tt]gemessen werden kann.
€dit: Es zeigt sich, dass es sinnvoll ist [tt]zmax=\zMax[/tt] zu setzen, dazu kann der maximale z-Wert in der Form
[tt]\pgfplotstablegetrowsof{\datatable}
\pgfmathtruncatemacro{\RowsNo}{\pgfplotsretval-1}
%Zeilenzahl: \RowsNo
\pgfmathsetmacro\zMax{0}
\foreach \n in {0,...,\RowsNo}{
\pgfplotstablegetelem{\n}{Z}\of{\datatable}
\pgfmathparse{\pgfplotsretval > \zMax ? \pgfplotsretval : \zMax}
\xdef\zMax{\pgfmathresult}
}
%Maximalwert z-Achse: \zMax[/tt]
ermittelt werden.
[attachment=0]55555a5.png[/attachment]
[code]\documentclass[border=5pt, tikz]{standalone}
\usepackage{pgfplots}
\usepackage{pgfplotstable}
\pgfplotsset{compat=1.17}
\usetikzlibrary{calc}
\def\pgfmathsetglobalmacro#1#2{\pgfmathparse{#2}%
\global\let#1\pgfmathresult}
\pgfplotsset{
colormap = {mycolormap}{
color(0) = (blue!50!black);
color(1) = (purple);
color(2) = (green!55!black);
color(3) = (brown);
color(4) = (blue!66)
color(5) = (violet)
},
colormap name=mycolormap,
%colormap name=viridis
}
\begin{document}
\pgfplotstableread[col sep=comma,header=true]{
X, Y, Z
2, 0, 4
1, 0, 5
0, 1, 10
3, 1, 1
1, 1, 3
2, 1, 0
1, 2, 0
2, 2, 5
2, 3, 6
1, 4, 7
1, 5, 11
}{\datatable}
% z-Maximum determination ==================
\pgfplotstablegetrowsof{\datatable}
\pgfmathtruncatemacro{\RowsNo}{\pgfplotsretval-1}
%Number of rows: \RowsNo
\pgfmathsetmacro\zMax{0}
\foreach \n in {0,...,\RowsNo}{
\pgfplotstablegetelem{\n}{Z}\of{\datatable}
\pgfmathparse{\pgfplotsretval > \zMax ? \pgfplotsretval : \zMax}
\xdef\zMax{\pgfmathresult}
}
%Maximum z-Axis: \zMax
% ============================
\begin{tikzpicture}[]
\begin{axis}[
%height=2cm, width=7cm,
% view={120}{40}, x dir=reverse,
xmin=0,
ymin=0,
zmin=0, zmax=\zMax,
enlarge z limits={rel=0.25,upper},
xtick={1,...,10},
ytick={1,...,10},
%ytick={0,25,...,100},
grid=both,
xlabel={$x$}, ylabel={$y$}, zlabel={$z$},
minor z tick num=1,
point meta=explicit,
scatter/use mapped color={draw=mapped color!50!black,
fill=mapped color!70},
]
% unitlenghth z-Axis determination
\path let \p1=($(axis cs:0,0,1)-(axis cs:0,0,0)$) in
\pgfextra{ \pgfmathsetglobalmacro{\zunitlength}{\y1} } node[xshift=2cm, yshift=2cm]{%\zunitlength % show value
};
\addplot3[
scatter, only marks,
mark=cube*, mark size=5, %opacity=0.8,
nodes near coords*=, % will er...
%%% barheight determination
visualization depends on={\thisrow{Z} \as \zvalue},
scatter/@pre marker code/.append style={
/utils/exec=\pgfmathsetmacro{\barheight}{\zunitlength*\zvalue},
/pgfplots/cube/size z=\barheight
},
] table[x=X, y=Y,
z expr={0.5*\thisrow{Z}},
meta expr={\thisrow{Y}}
]{\datatable};
\end{axis}
\end{tikzpicture}
\end{document}[/code]