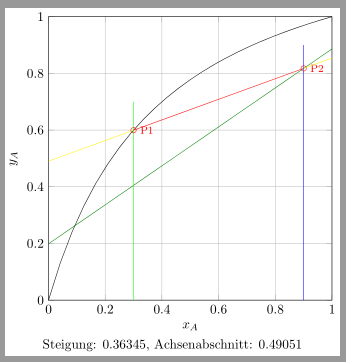
Leider verrätst Du nicht, was Du mit Steigung und Achsenabschnitt dann tun willtst.
\documentclass{standalone}
\usepackage[utf8]{inputenc}
\usepackage{pgfplots}
\pgfplotsset{compat=newest}
\usetikzlibrary{math, calc, intersections}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
domain=0:1,
height=9cm,
width=9cm,
xlabel={$x_A$},
ylabel={$y_A$},
grid=major,
clip=false,
xmin=0, xmax=1,
ymin=0, ymax=1
]
\addplot[mark=none, name path=A]{3.5*x/(1+2.5*x)};
\addplot[green!50!black, mark=none, name path=B]{0.6876*x+0.19875};
\draw[blue, mark=none, name path=C](0.9,0) -- +(0,0.9);
\draw[green, mark=none, name path=D](0.3,0) -- +(0,0.7);
\path [name intersections={of=A and D,by=P1}];
\draw [red] (P1) circle[radius=2pt] node [xshift=10pt] {\footnotesize {P1}};
\path [name intersections={of=B and C,by=P2}];
\draw [red] (P2) circle[radius=2pt] node [xshift=10pt] {\footnotesize {P2}};
\draw[red](P1) -- (P2)\pgfextra{\pgfgetlastxy{\xii}{\yii}};
\path let \p1=(P1), \p2=(P2) in \pgfextra{%
\pgfmathparse{(\y2-\y1)/(\x2-\x1)} \xdef\steigung{\pgfmathresult}%
\pgfmathparse{\y1-\steigung*\x1} \xdef\achsenabschnitt{\pgfmathresult}%
};
\draw[yellow](0pt,\achsenabschnitt pt)--(P1);
\draw[yellow](P2)--(210.5pt,210.5pt*\steigung+\achsenabschnitt pt);
\end{axis}
\node[below]at(current axis.outer south){Steigung: \steigung, Achsenabschnitt: {\achsenabschnitt} pt};
\end{tikzpicture}
\end{document}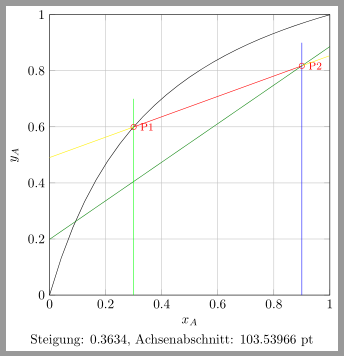
Beachte dabei, dass \achsenabschnitt hier den Abstand des Schnittpunktes der Geraden mit der y-Achse vom Nullpunkt in pt angibt. Das hat also nichts mit den Einheiten zu tun, die an der Skale stehen. Ähnliches gilt für den Anstieg. Der enspricht nur dem Anstieg in der Geradengleichung, wenn eine y-Einheit genau so lang wie eine x-Einheit ist.
Wenn Du den Achsenabschnitt umrechnen möchtest, dann gib einen Wert für die x- und y-Einheiten vor:
\documentclass{standalone}
\usepackage[utf8]{inputenc}
\usepackage{pgfplots}
\pgfplotsset{compat=1.14}
\usetikzlibrary{math, calc, intersections}
\pgfplotsset{compat=newest}
\begin{document}
\begin{tikzpicture}
\newcommand*\plotunit{7.5cm}
\begin{axis}[
domain=0:1,
x=\plotunit,
y=\plotunit,
xlabel={$x_A$},
ylabel={$y_A$},
grid=major,
clip=false,
xmin=0, xmax=1,
ymin=0, ymax=1
]
\addplot[mark=none, name path=A]{3.5*x/(1+2.5*x)};
\addplot[green!50!black, mark=none, name path=B]{0.6876*x+0.19875};
\draw[blue, mark=none, name path=C](0.9,0) -- +(0,0.9);
\draw[green, mark=none, name path=D](0.3,0) -- +(0,0.7);
\path [name intersections={of=A and D,by=P1}];
\draw [red] (P1) circle[radius=2pt] node [xshift=10pt] {\footnotesize {P1}};
\path [name intersections={of=B and C,by=P2}];
\draw [red] (P2) circle[radius=2pt] node [xshift=10pt] {\footnotesize {P2}};
\draw[red](P1) -- (P2)\pgfextra{\pgfgetlastxy{\xii}{\yii}};
\path let \p1=(P1), \p2=(P2) in \pgfextra{%
\pgfmathparse{(\y2-\y1)/(\x2-\x1)} \xdef\steigung{\pgfmathresult}%
\pgfmathparse{(\y1-\steigung*\x1)/\plotunit} \xdef\achsenabschnitt{\pgfmathresult}%
};
\draw[yellow](0pt,\achsenabschnitt)--(P1);
\draw[yellow](P2)--(1,\steigung+\achsenabschnitt);
\end{axis}
\node[below]at(current axis.outer south){Steigung: \steigung, Achsenabschnitt: \achsenabschnitt};
\end{tikzpicture}
\end{document}